This is part of my Best of the Web series, where I scour the Internet for the best free activities available today. By best, I’m looking for activities that engage the class with interesting puzzles and meaningful learning. Two posts from Dan Meyer help clarify: Culture Beats Curriculum and Real Work vs. Real World.
#1: Desmos Quadratic Bundle
Whenever Desmos has a bundle of activities on a topic, it’s worth a good look. Thequadratic bundle is no exception. (I couldn’t stop playing through the entire Marbleslides challenge… and only wish I could link here to show my favorite creations.) Desmos specializes in building conceptual understanding of functions, particularly between graphical and algebraic representations. The bundle currently has the following activities, each of which take between 30 and 60 minutes to complete.
- Will It Hit the Hoop? – Develop a need for quadratics by modeling basketball shots with linear and quadratic functions (drawn from Dan Meyer’s activity posted here)
- Polygraph: Parabolas – Understand and describe key features of linear systems
- Polygraph: Parabolas, Part 2 – Reinforce academic vocabulary used to describe parabolas
- Match My Parabola – Combine knowledge of intercept, vertex, and standard form with principles of transformations to build equations passing through sets of 3 points
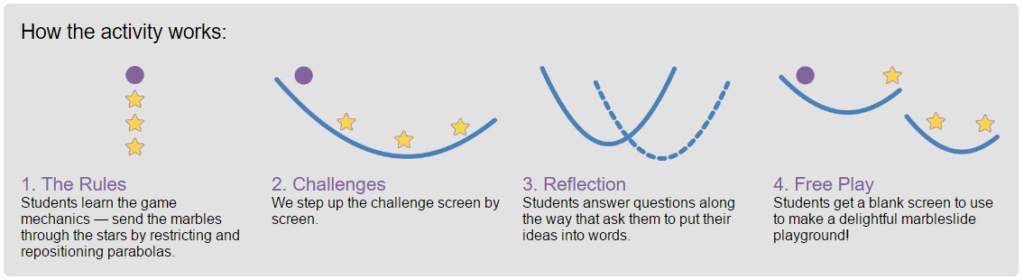
- Marbleslides: Parabolas – Create graphs to destroy sets of stars in an addictive, challenging activity (a personal favorite… and I’m in good company!)
- Card Sort: Parabolas – Practice sorting, creating, and interpreting parabolas
- Penny Circle – This is a wonderful activity, but I prefer saving it for a future lesson on choosing the right model for a scenario
Polygraph works best with a device for each student and Marbleslides would work best for a device per group, but with a touch of creativity the rest can work with a single projector and whiteboard for the class. Here’s the link: Desmos – Quadratic Bundle.
#2: World Record Airbag
Quick and simple, the World Record Airbag is a 3 Acts Math problem that creates Dan’s essential intellectual need to know. The first video shows a man jumping off a tall tower with nothing–no parachute, no bungee cord, no magic squirrel suit–and aiming for an airbag far below. As he hits it, the narrator cuts out just as he tries to say how fast the man was falling when he landed. Enter Act 2: figuring out what you need to know to find the answer. Once they think they have it, show Act 3. Here’s the link: Quadratic Modeling – World Record Airbag.
If you want to take this idea to another level, I have a feeling you could rig the Barbie Zipline lessons to test some great questions. For example, what happens to the time it takes Barbie to hit the ground based on her starting height, assuming the angle of descent is fixed? What happens to the time it takes to hit the ground if the starting height is fixed but the angle of descent changes? This would be a great opportunity for students to develop testable hypotheses, collect data, run regressions, and see what models fit the data best!
#3: Classic Quadratics… Pumpkin Catapults
Once they’re ready for regressions, it’s time for the magic of medieval mathematics. There are three ways to do this.
- The easy way: Give students a scenario, guided questions, and set them loose. Here’s a heavily guided example of this approach: Pumpkin Catapult Parabola Activity (this will download as a PDF).
- The less easy way: Give them a sample data and ready-to-go questions, but this time have students run a regression too find the equation. Houston ISD posted a great example which also includes several other quick application problems here: Houston ISD on Quadratic Regressions.
- The boom-goes-the-dynamite way: Have students build and analyze their own catapults. With a few prepared materials, the construction won’t take too long. Sean Sweeney lays out a great implementation here: Sweeney Math M&M Catapult Project. (If you’re feeling bold, you can take one step further and introduce a new variable–the length of the catapult arm. Students can see how the length of the arm impacts the distance, vertical velocity upon release (linked to time in the air) and–if you’re extra bold–even horizontal velocity!)
If you’re ever struggling to find a video to anchor a catapulting lesson, this may be the one: The Amazing Race – Watermelons Challenge.
#4: ChalkDoc Quadratic Activities
For the record, I love quadratics–the model of what goes up must come down. My favorite method introduce quadratics is this this one: Quadratics Sample Hack. This is a simple way to let students develop a pattern-based understanding of the connection between graphs and their algebraic representations before we agree on the formal rules of a new topic.
Once students get the hang of it, I like to mess with them. My favorite analysis activity is The Case of Aaron Rogers, where we pose this question: Does the career of professional athletes rise and fall like a parabola? Do they rise from their raw rookie state to greatness… only to slip back down as they get too old to keep up? It’s a full class activity that starts by interpreting a simple model, then moves to creating a precise model, then analyzes some of the big questions. If you want to add more big questions, it’s in an editable Word form. And a disclaimer: Credit to Question 1 goes to the ever talented Ms. Stephens. Here’s the link: Parabola Activity: The Case of Aaron Rogers.
See more activities like this available (for free) in the ChalkDoc system!
We also offer lots of quick, free problems for creating, solving, and analyzing quadratic equations that you can steal to build customized activities, worksheets, homework, and tests. Here’s an example: ChalkDoc – Analyzing Quadratic Equations.
Tell Me What’s Missing!
I’ll update this post as new, helpful resources emerge. If you have any thoughts, suggestions, questions, or requests, please let me know!
P.S. Yes, the header image is of the Gateway Arch in St. Louis. No, it’s not really a parabola. It’s admittedly more complicated than that…